考點:排列組合.
分析:我們把學學洗的5個碗過程看成從起點向右走5步(即洗幾個碗就代表向右走幾步),思思拿5個碗的過程看成是向上走5步(即拿幾個碗就代表向上走幾步),摞好碗的摞法,就代表向右、向上走5步到達終點最短路線的方法.由于洗的碗要多余拿的碗,所以向右走的路線要多余向上走的路線,所以我們用下面的斜三角形進行標數,共有42種走法,即代表42種摞法.
解答:解:根據對應關系,再運用階梯型標數法畫圖如下:
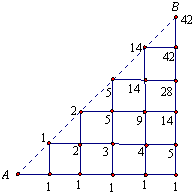
答:共有42種摞法.
點評:本題考查了利用“階梯型標數法”進行復雜的排列組合,關鍵是確定橫格和縱格的格數。
編輯推薦



